[LG]《Topos Causal Models》S Mahadevan [Adobe Research] (2025)
拓扑范畴因果模型(Topos Causal Models, TCMs)提出了将因果推理置于拓扑范畴理论框架下的新范式,具备以下关键特点:
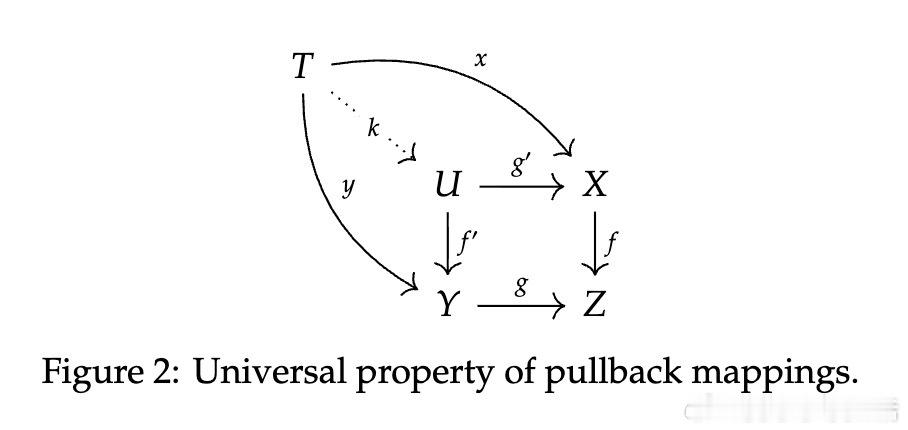
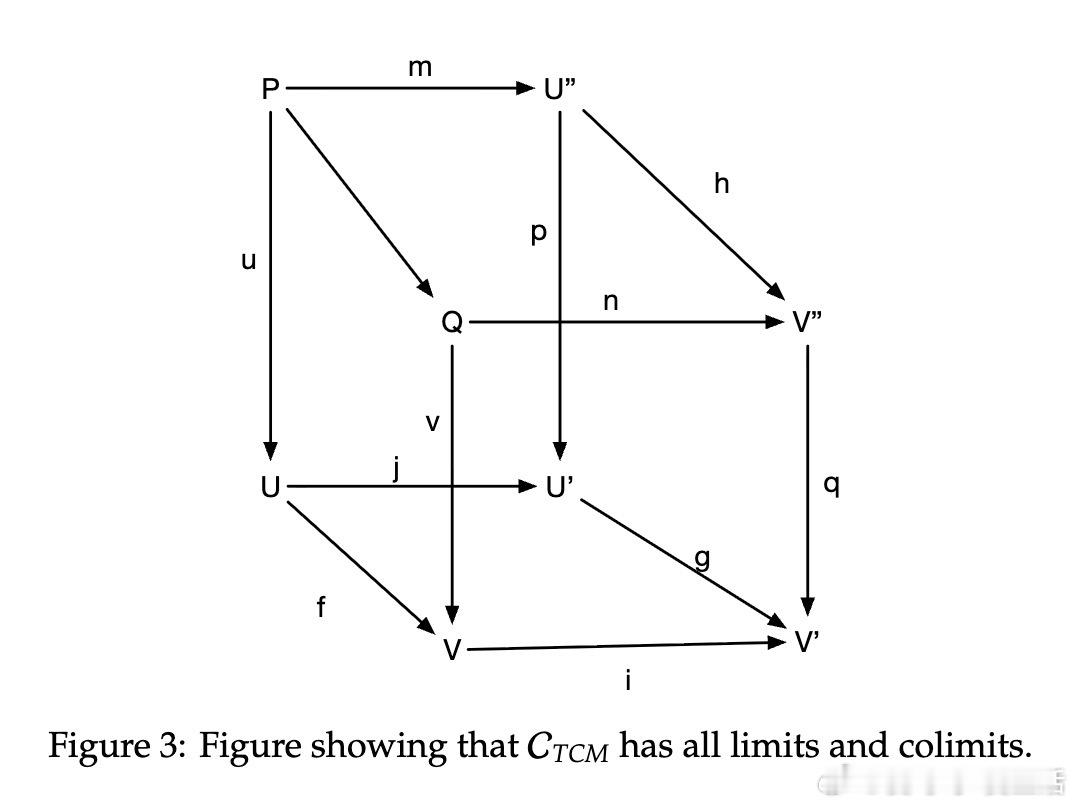
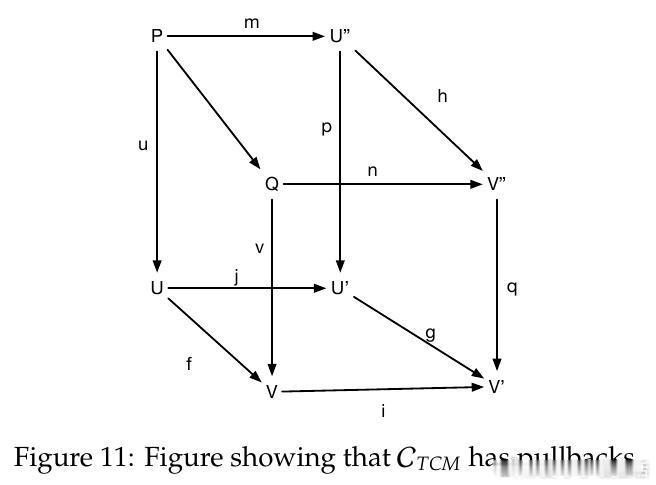
• (Co)complete 性质:TCM 所在范畴拥有所有极限与余极限,保证任意复杂因果图都存在“解”,即极限或余极限形式的全局函数近似,从而使因果模型的组合与逼近成为可能。
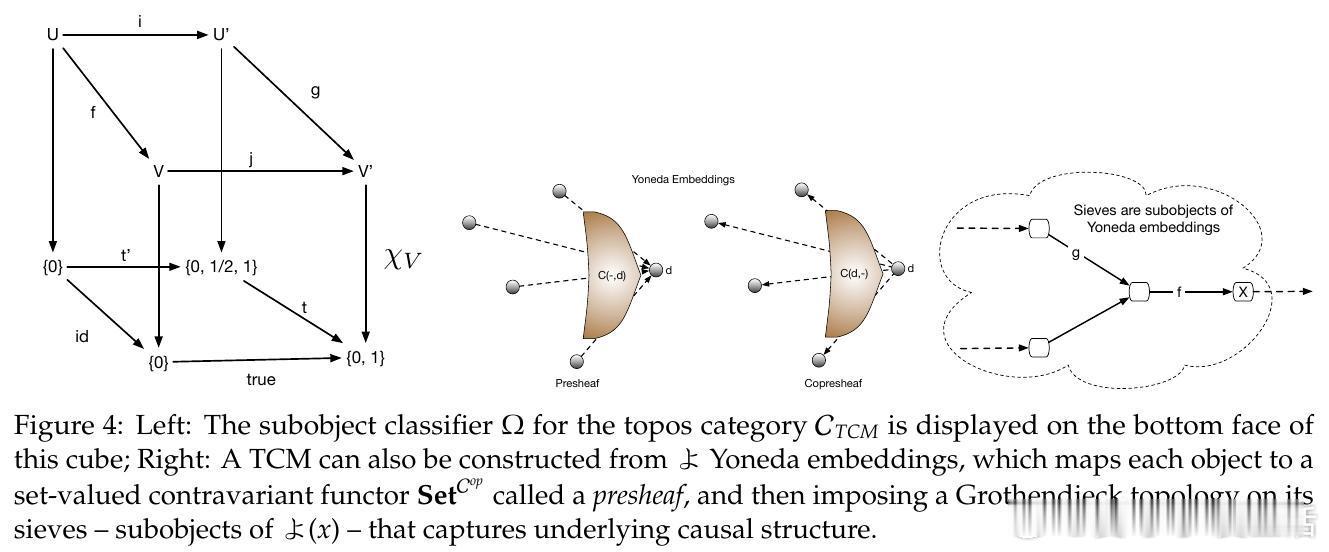
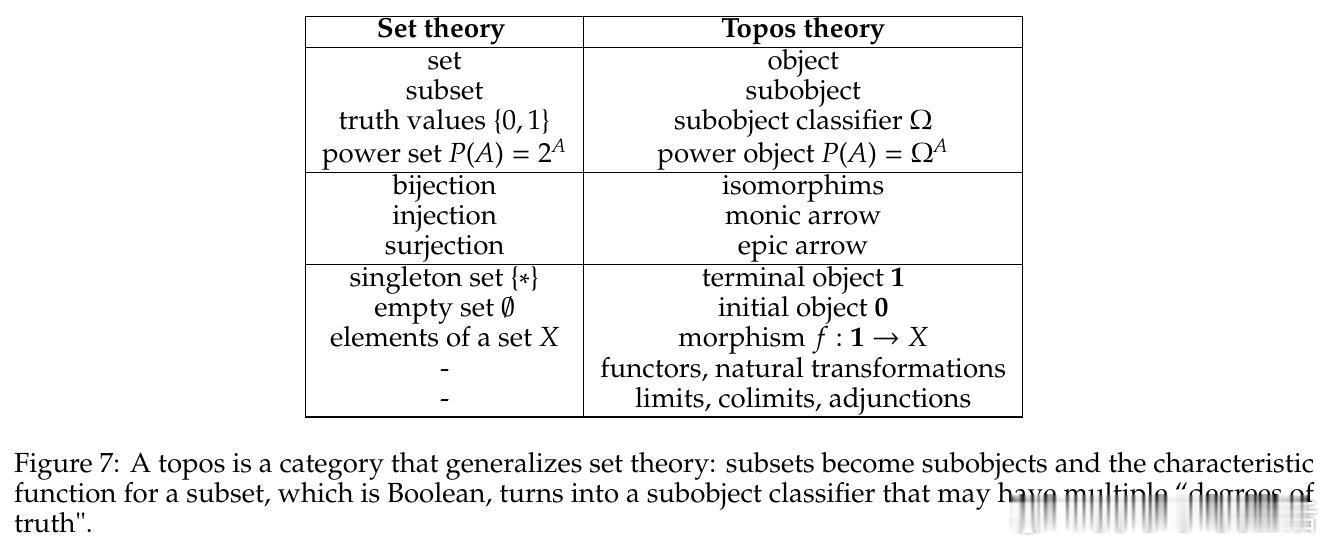
• 子对象分类器(Subobject Classifier):以范畴论的单射箭头(monic arrows)构建子模型,精确定义因果干预操作,推广了 Pearl 的 do-演算,且其真值不再是传统的布尔值,而是多值的直觉主义逻辑(Heyting 代数),这为因果干预提供了更丰富的逻辑语义。
• 指数对象(Exponential Objects):支持对因果模型的等价类、因果同伦(causal homotopy)和边覆盖反转(covered edge reversal)等操作进行形式化推理,拓展了结构因果模型(SCMs)的表达能力。
• 内部逻辑与语义:TCMs 作为拓扑范畴,配备 Mitchell-Bénabou 语言及其 Kripke-Joyal 语义,可在范畴内部进行因果及反事实推理,提供了基于类型逻辑的因果模型语言,兼具严谨性与表达力。
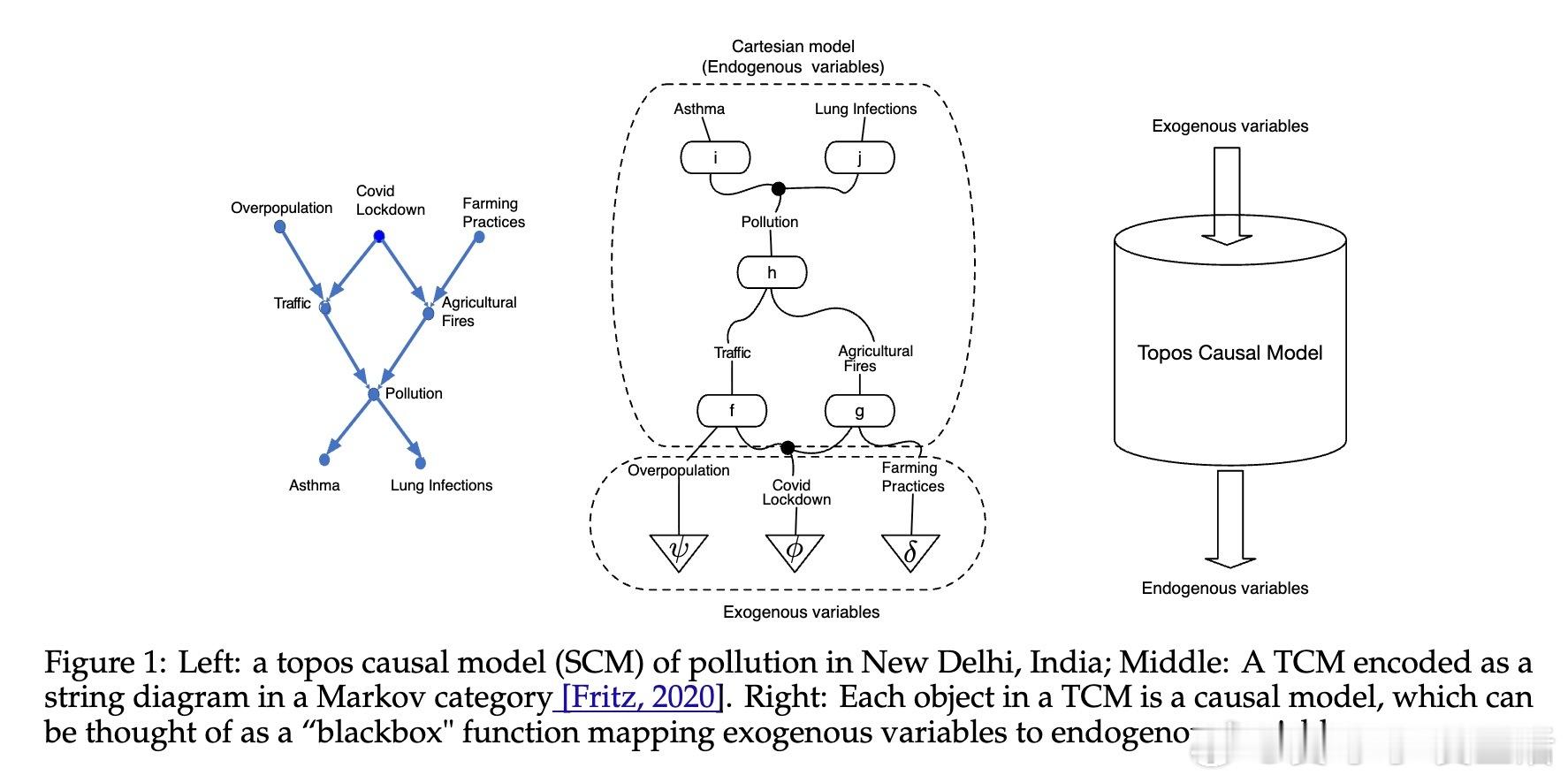
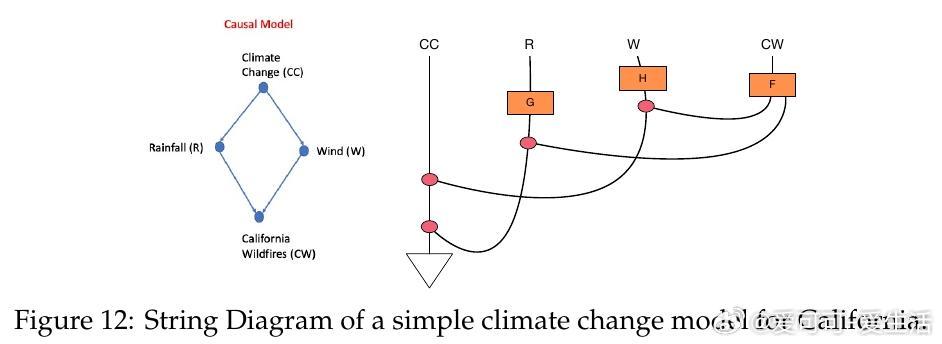
• 泛化性强:结构因果模型(SCMs)、贝叶斯网络、Markov 范畴及单纯复形(simplicial sets)等均可视为 TCM 的特例,且均形成拓扑范畴,统一了多种因果建模方法。
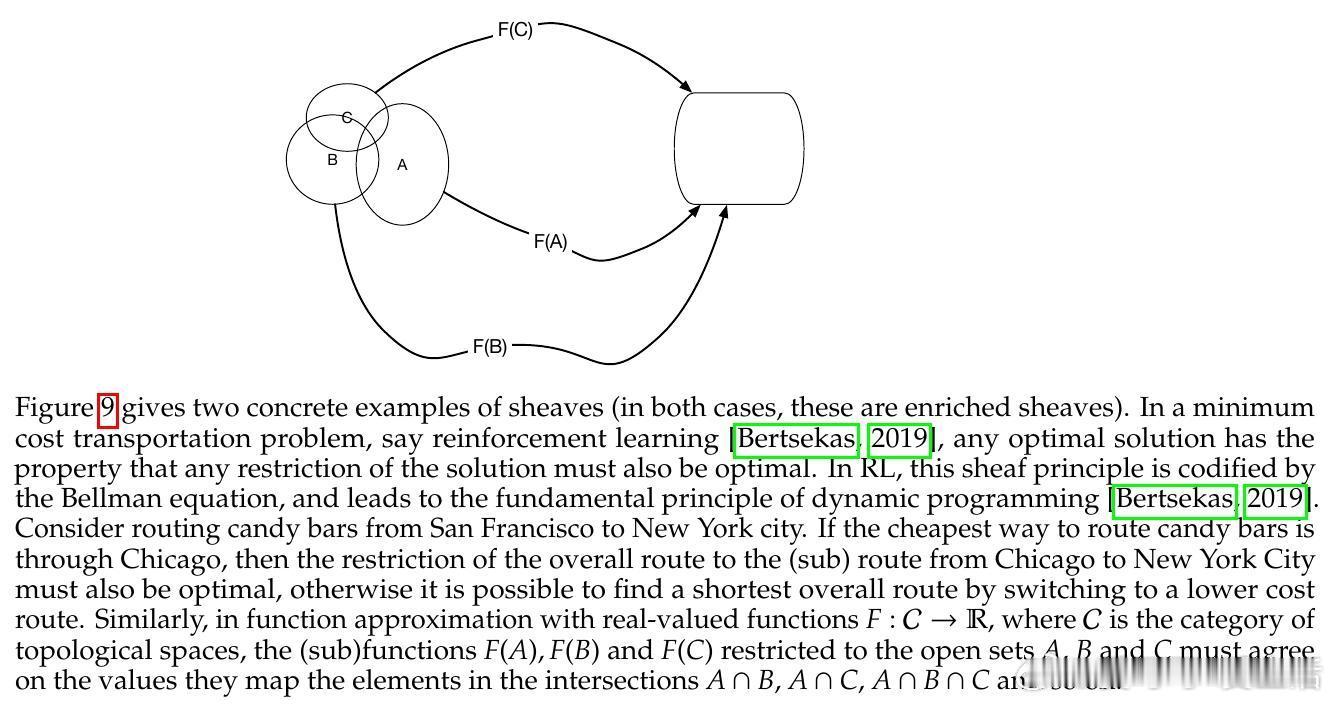
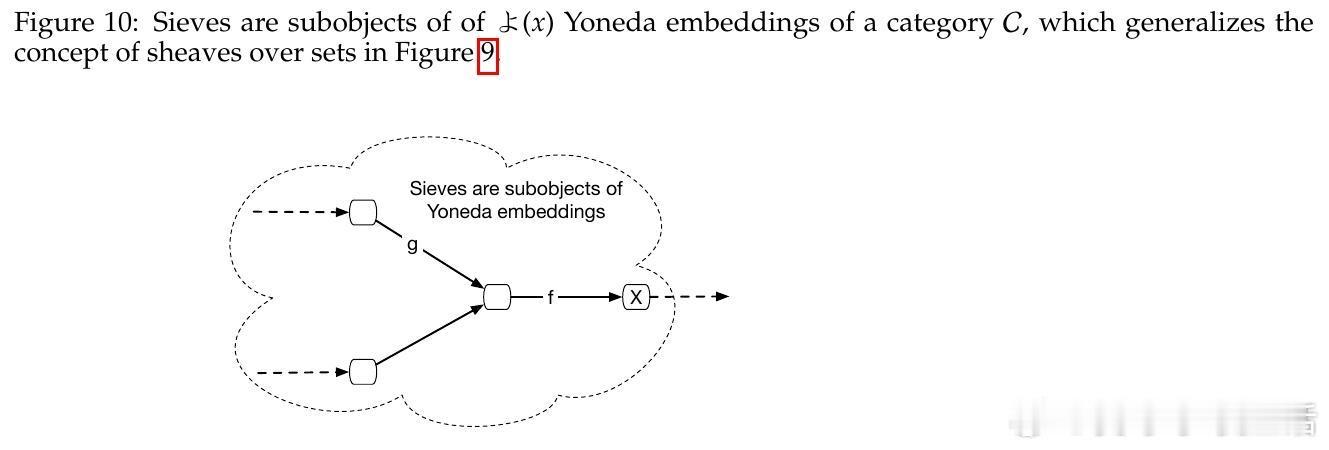
• 基于 Yoneda 嵌入与 Grothendieck 拓扑的剪切理论(Sheaves),实现局部因果机制到全局因果函数的唯一拼接,解决因果机制组合的数学难题。
• 因果推理的新视角:通过范畴的极限、余极限、单射箭头及指数对象,重新定义因果近似、因果干预和因果等价,为因果发现和反事实分析提供了强大工具。
未来方向包括利用范畴同伦理论研究因果模型等价类、深入挖掘内部逻辑在反事实推理中的应用,以及探索极限与余极限在因果模型逼近中的作用。
🔗 arxiv.org/abs/2508.08295
因果推理拓扑范畴范畴论结构因果模型机器学习人工智能