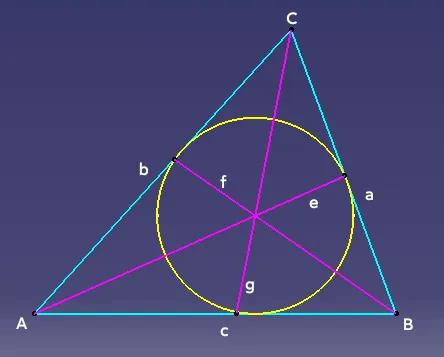
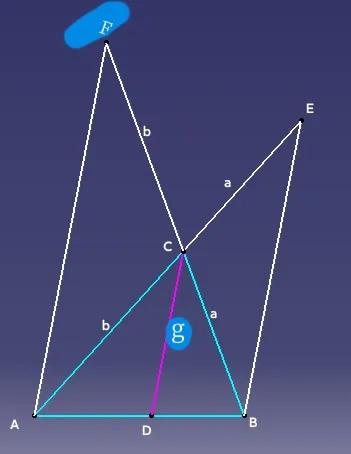
构造相似三角形证明线段不等式 如图,设△ABC三边为a、b、c,其所对应的内角平分线分别为e、f、g,则有1/a+1/b+1/c<1/e+1/f+1/g。 线段不等式自然想到三角形两边之和大于第三边,当然这种式子形式也让人想到方程x+y=a,y+z=b,z+x=c。同时,倒数形式又让人联想到成比例线段,即相似三角形。 如图二,设CD平分∠ACB,则CD=g,过A、B作CD平行线,分别与BC、AC延长线交于F、E。 易得CE=BC=a,CF=AC=b,且△ABE∽△ADC,△BCD∽△BFA。所以CD/BE=AD/AB,CD/AF=BD/AB,两式相加可得CD/BE+CD/AF=(AD+BD)/AB=1,两边同除以CD可得1/BE+1/AF=1/CD,根据三角形两边之和大于第三边,所以BE<2a,AF<2b,代入上式可得1/g>1/(2a)+1/(2b)。 同理可得1/e>1/(2b)+1/(2c) 1/f>1/(2a)+1/(2c) 三者相加可得 1/a+1/b+1/c<1/e+1/f+1/g