利用正三角形性质构造全等三角形解题 如图一，四边形ABCD中，BC＞CD＞AD，O为AB中点，且满足∠AOD=∠COB=60°，求证：CD+AD＞BC。 如图二，在CO上取OE=OD，连接DE与BE，则△ODE为等边三角形，所以OD=OE，又∠AOD=∠COB=60°，AO=BO，所以△AOD≌△BOE，所以AD=BE，在△CED中，由于∠CED=120°所以CD＞CE(大角对大边)，在△BEC中，BE+CE＞BC，所以AD+CD＞BC。
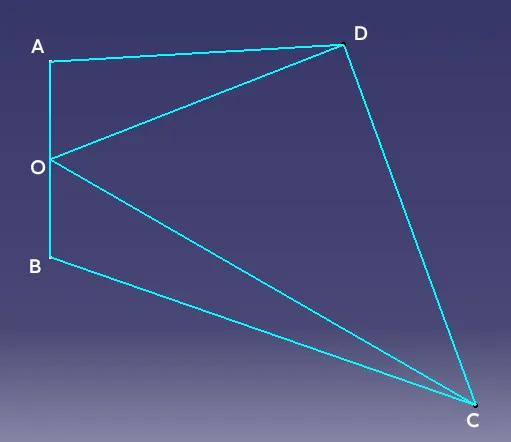
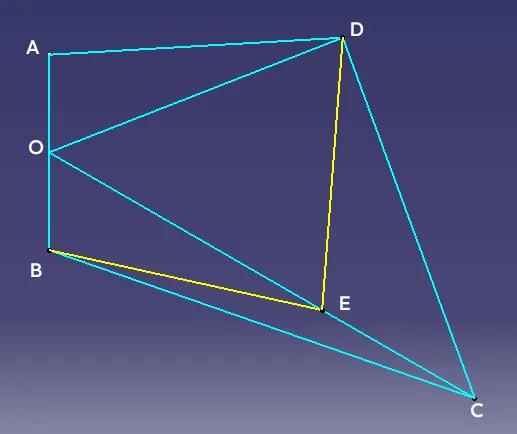
利用正三角形性质构造全等三角形解题 如图一，四边形ABCD中，BC＞CD＞AD，
裕耀看看课程
2025-04-03 08:38:37
0
阅读：6
