妙用旋转解题 如图一，凸四边形ABCD中，AB=AD，∠DAB=60°，∠BCD=120°，则有AC=BC+DC。 当然这题可以用托勒密定理解，因为ABCD是圆内接四边形，连接BD，有AB·CD+BC·AD=AC·BD，因为△ABD为等边三角形，所以AB=AD=BD，代入托勒密式子约掉AB、AD与BD即可得出AC=BC+DC。 如果利用旋转全等变换，也很简洁，如图二，把△ACD绕点D旋转60°，变为△BED，△DCE自然为等边三角形，所以BE=AC=BC+CE=BC+CD。
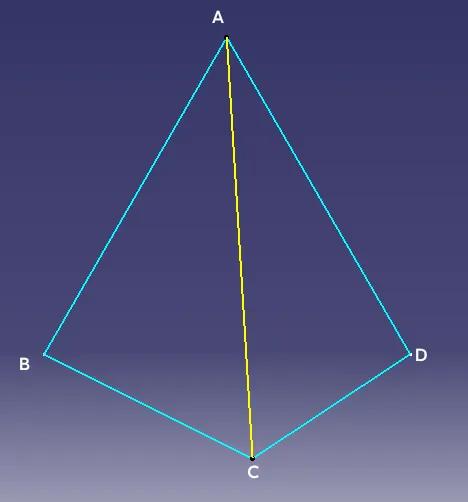
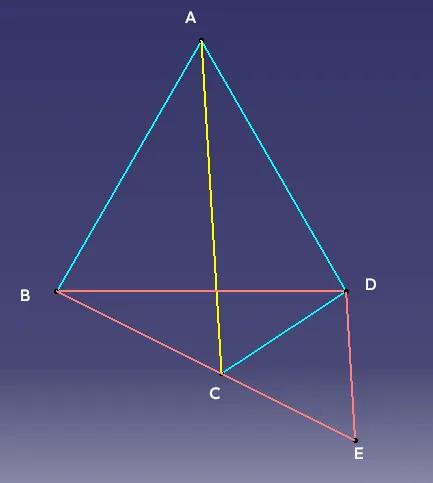
妙用旋转解题 如图一，凸四边形ABCD中，AB=AD，∠DAB=60°，∠BCD
裕耀看看课程
2025-03-31 07:54:45
0
阅读：15
