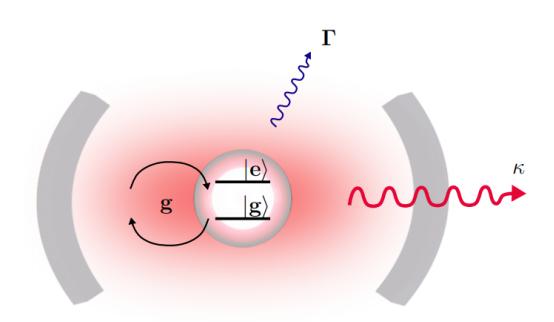
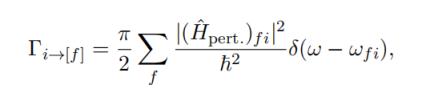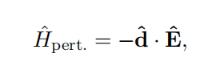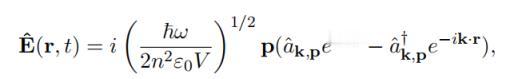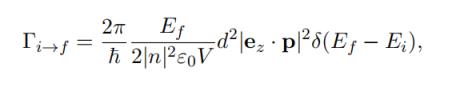空腔内量子点的自发发射有着怎样的原理? 当量子点(QD)处于激发态时,光与物质的相互作用会通过自发辐射产生到基态的弛豫过程,释放光子场。然而,QD作为一个点发射体,辐射角度范围广,从而降低了光的收集效率。 在体块半导体中,另一个现象进一步降低了光的收集效率:光的全内反射。由于GaAs和空气之间的折射率差异,光会在界面上反射。这两个因素的结合导致了较低的光子收集效率,最多仅达到约2%的效率。 尽管光子收集效率对于本博士研究中进行的实验研究并非根本性关键属性,但它被证明对于实验至关重要。我们研究了将QD耦合到单个腔模的样品,从而实现了我们研究的重要可实现特性。首先,这种耦合导致对QD发射的高效收集,并且允许高检测速率,这对于使我们所提出的大多数研究可行至关重要。 其次,通过强迫QD在电磁场的明确定义模式中发射,我们的系统接近于所谓的一维原子的教科书情况。最后,通过加速自发辐射,与QD环境的相互作用被大大抑制,而我们研究的核心——相干性得到了极大增强。 为了理解将量子点(QD)耦合到腔中如何改变发射动力学,首先我们讨论量子点在体块材料中的自发辐射。 在一个一般的图景中,我们考虑一个二能级系统,即一个位于r = 0处的点偶极子,被连续均匀的介质材料(这里是GaAs)所环绕。通过一个光脉冲,我们以频率ω0共振激发这个二能级系统,使得产生了粒子反转,从而占据了激发态。 一旦量子点被激发,光激发脉冲立即关闭,使得围绕量子点的电磁场处于真空态。经过一定时间,量子点的激发态人口开始衰减回到基态。这种人口转移通过自发辐射转移到电磁场上,产生了光子场-电磁场的激发态,具有波矢k和偏振p。可以使用摄动理论计算过渡速率或衰减速率,利用费米黄金法则: 其中,i表示初始态 |i⟩ = |e, 0⟩(原子处于激发态,无光子),f表示可访问的最终态 |f⟩ = |g, k, p⟩(原子处于基态,光子处于模式k、p中),ˆHpert.表示摄动哈密顿量,ω表示辐射的频率,ωf i表示原子的跃迁频率。对量子点-体块系统的可能最终态求和,得到了体块自发辐射速率Γbulksp。 其中,dˆ是偶极子算符,电场算符在二次量子化框架中给出:其中,aˆk,p和aˆ†k,p是模式{k, p}中的湮灭和产生算符。此外,我们还有介质的特定参数ε0、n,分别是介电常数和折射率。我们还识别出量子化体积V = L3。 沿着偶极方向的单位矢量,我们可以通过注意到GaAs在900 nm处的实部折射率为3.5,而虚部接近于零,来简化这个跃迁速率。此外,我们知道每个波矢k具有两个可能的正交极化态p1、p2,但我们可以选择它们使得其中一个与偶极方向正交,从而导致一个单独的极化态对发射场产生贡献:|ez ·p|2 = sin2θ,其中θ是偶极和波矢之间的角度,参见图片,在原点处有一个指向z方向的偶极。 如前所述,自发辐射速率之和导致了体块自发辐射速率。更准确地说,这个求和应该被一个关于所有可能能量和固体角Ω的积分所替代,这个积分由态密度ρ(Ω, E)加权。 其中dN是在能量范围[E, E + dE]内的态的数目,其波矢k沿着固体角dΩ指向。在极坐标中,积分的积分体积为(k = k(sin θ cos ϕ, sin θ sin ϕ, cos θ)),得到所有可能的发射模式中的总自发辐射速率的表达式为d3k = k2dkdΩ,其中dΩ = sin θdθdϕ是围绕k方向的固体角元素。 从中我们还可以得到体块中激子的辐射寿命T = (Γbulksp)−1,对于GaAs中的InGaAs量子点,波长为930 nm,大约为1 ns。 对于应用目的,高度希望控制量子点的发射。腔量子电动力学(cQED)提供了一种解决方案,我们知道将一个二能级系统耦合到腔中将改变发射速率进入腔模式。在本节中,我们讨论将量子点耦合到腔中如何强烈改变发射动力学,并且可能导致自发辐射速率的剧增,即所谓的Purcell效应。 我们考虑一个位于腔内的二能级系统,参见图片。两能级系统与腔模式之间的耦合常数用参数g表示。其他重要的量子点-腔参数包括腔阻尼率κ,描述光子从腔中逃逸的速率,以及发射体的总相干失相速率Γ。后者是自发辐射衰变速率γ(包括腔外模式)和纯失相速率γ之和:Γ = γ² + γ。 就耦合强度而言,我们可以区分两种情况:强耦合和弱耦合。在强耦合情况下,当g > |κ−γ|/4时,自发辐射会发生在两个不同的频率上,或者在弱耦合情况下,当g < |κ−γ|/4时。在第一种情况下,一旦激发,二能级系统可以在多个周期内发射和吸收光子,直到光子离开腔体:系统呈现真空拉比振荡。