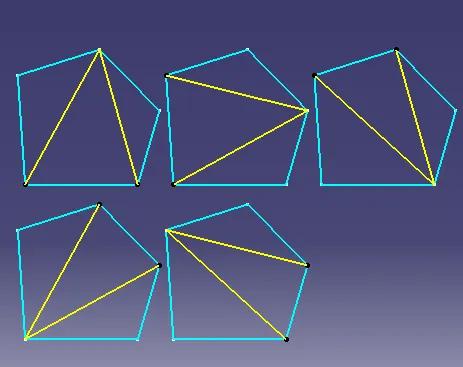
1751年,欧拉曾提出一个切割多边形问题:一个平面凸多边形,利用对角线切割成三角形的方法有多少种? 首先三角形最简单,只有1种。 四边形呢,也简单,两条对角线都可以分割成三角形,所以有2种。 五边形,稍微复杂一点有5种,如图一 六边形就更复杂了,如图二。第一种情况,从每个顶点起,一共6种,图二-1;第二种情况,隔顶点分割,一共2种,图二-2;第三种情况,根据对边分割,一共3x2=6种,所以总共14种。 那么对于凸n边形的分割方法Dn有多少种呢?后来数学家乌尔班找到了比较简洁的递推公式Dn+1/ Dn=(4n-6)/n。 例如n=3时,D4=1x(4x3-6)/3=2 n=4时,D5=2x(4x4-6)/4=5 n=6时,D7=14x(4x6-6)/6=42。