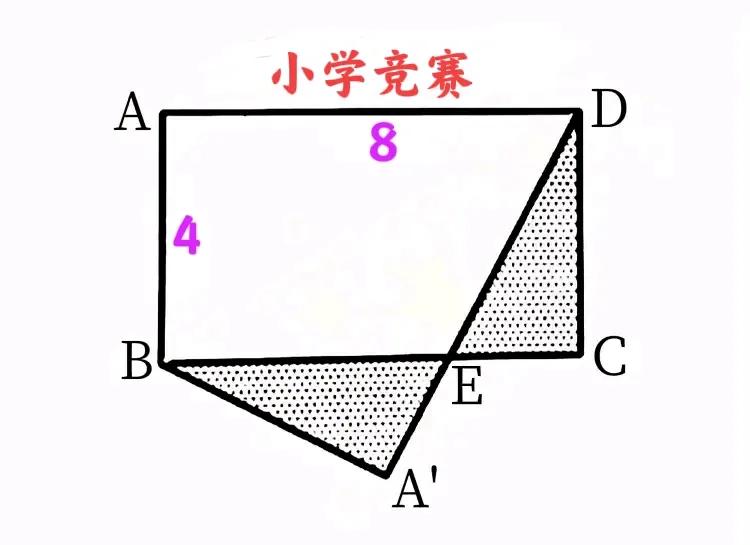
“团灭，一个不剩！”有人说严重超纲！这是一道小学数学竞赛题：长方形折叠所成三角形面积，其三边边长均未知！ 如图，长方形ABCD的长宽分别为8和4，将其沿对角线BD翻折，记翻折后的点A记为A'，A'D与BC相交于点E，求阴影部分面积之和。 难点：如何不超纲求出BE和CE？ 提示：连接BD，BE=DE=5，CE=A'E=3。 #小学数学#
“团灭，一个不剩！”有人说严重超纲！这是一道小学数学竞赛题：长方形折叠所成三角形
贝笑爱数学
2024-07-30 18:24:50
0
阅读：570
嗄呗
用证明勾股定理的方法来解这道题，一点新意都没有，翻来覆去都是应用勾股定理的证明方法，既然这样，何不把勾股定理拿出来讲呢。
人公
他就怎么等于5的
滞空落叶 回复 09-29 12:06
从图中可以看出A'B=AB,A'D=AD连接BD后可得出A'BD和BDC面积相等，从而得到A'BE和CED面积也相等，根据三角形的面积计算公式可得A'E=CE。在三角形CED中利用勾股定理求出CE=3，DE=5。
喂，是你
∵A，B=CD,三个角相等，∴三角形全等。4²+ce²=(8-ce)² ce=3 s新=3*4=12
青山医院陈主任
勾股定理是二次方程式吧，小学有吗？
雷勇
得8
D_jiahe
345勾股