🔮魔术的尽头是数学（北大数院详解

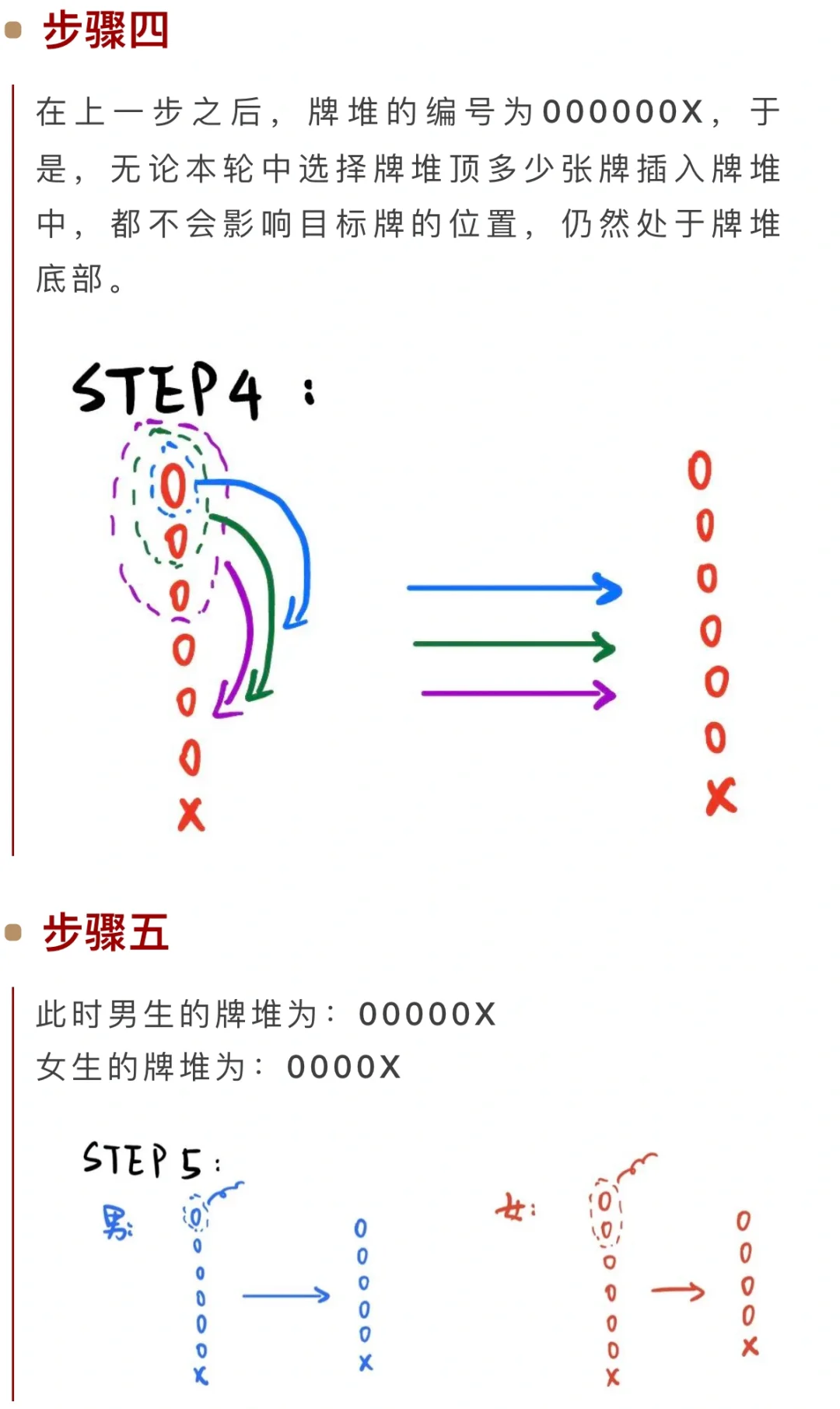
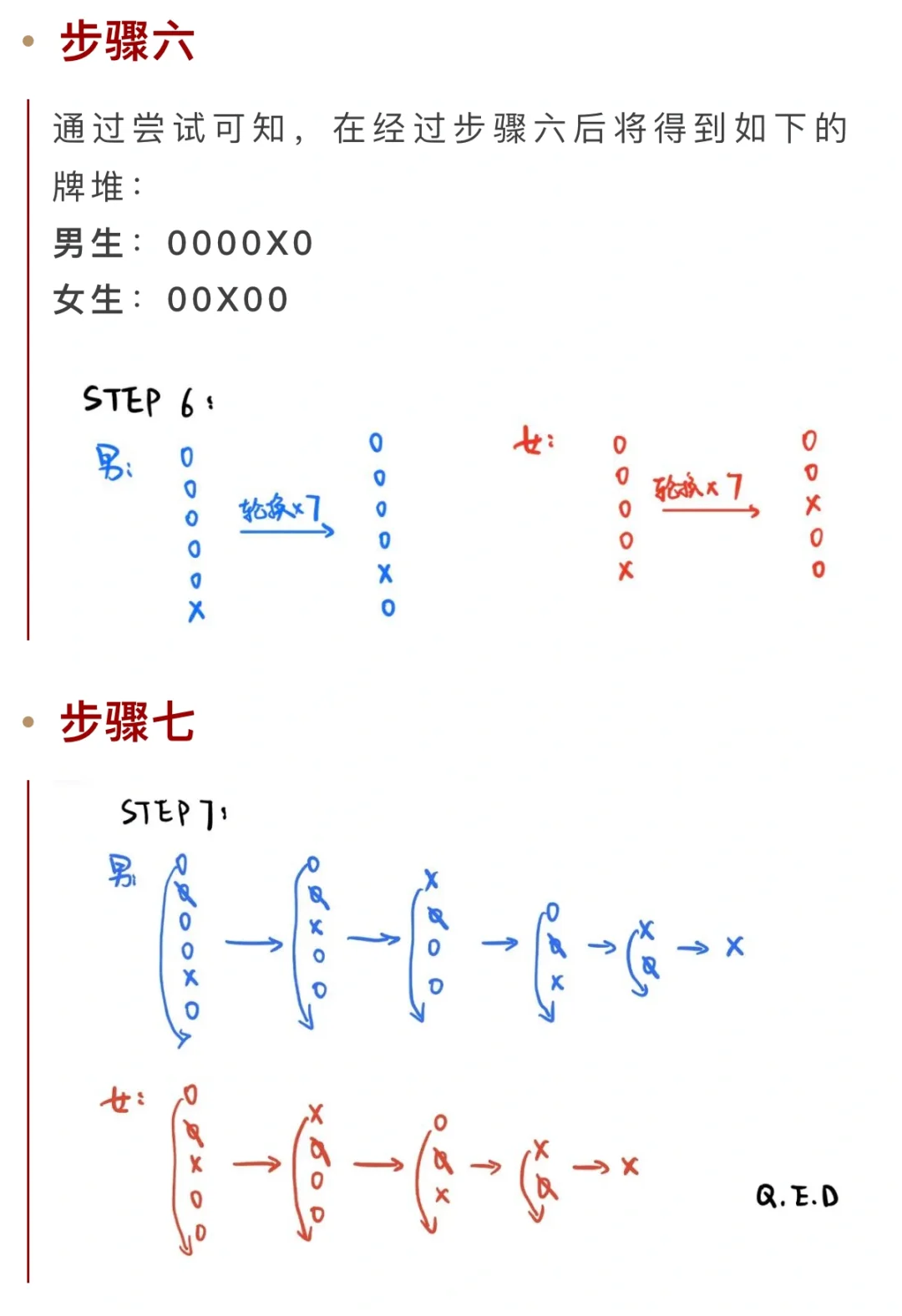
【约瑟夫问题】：设有编号为1，2，......，n的n个人围成一个圈，从第1个人开始报数，报到m时停止报数，报m的人出圈。再从他的下一个人起重新报数，报到m时停止报数，报m的出圈......按照这个规则进行下来，直到所有人全部出圈为止。求最后留下来的人编号。为了使问题简化，我们考虑n个人编号为0 ~ n-1的情况，每 m 个人退出一个人，我们称之为（n, m）问题。第一个人（即编号为在模n下同余m的人）退出之后，对剩下的 n-1 个人重新编号，则新问题的k号在原问题中对应 k+m 号。因此（n, m）问题的解 J (n, m) = J (n-1, m)+m 且 J (1, m) = 1（模n意义下）。据此，通过递推的方法可以得到 J (n, m)。在实践中，约瑟夫问题一般用代码进行求解。刘谦的魔术中使用的便是 m=2 的特殊情况。 ❤️这个魔术即将变成2024数学考题[偷笑R] 解题思路全由【北京大学数学科学学院】的同学们