不可能的遗产

1783年9月后的某一天，圣彼得堡科学院的秘书尼古拉斯·弗斯面临着一个行政上的噩梦。他打开了一个刚刚过世的老人的办公室大门，或者更准确地说，是仓库大门。

摆在弗斯面前的不是几十篇论文，也不是几百页手稿。是一座山。

这座纸山里堆积着关于流体力学、月球运动、造船技术、数论、光学、声学和人口统计学的计算结果。弗斯当时做了一个估算，如果科学院想要发表这些遗作，大概需要几年时间。

事实证明，弗斯是个不合格的预言家。

圣彼得堡科学院足足用了47年才把这些积压的纸张整理出版完毕。这期间，人类经历了法国大革命，拿破仑的崛起与流放，蒸汽机的普及，甚至连那个老人曾经效力的帝国都换了好几任沙皇。而那个老人的论文还在源源不断地从印刷机里吐出来，仿佛他从未停止过思考，只是不再需要进食和呼吸。

这个人就是莱昂哈德·欧拉。

但这个故事最让人费解的地方不在于他写了多少，而在于他是如何写出来的。在他生命最后这十几年里，这座纸山的大部分内容是在完全的黑暗中完成的。他看不见纸，看不见笔，甚至看不见自己刚写下的公式。

巴塞尔的意外

1707年，瑞士巴塞尔。保罗·欧拉牧师对自己儿子的未来有着清晰的规划。在这个加尔文教派的据点，没有什么比继承父业、成为一名乡村牧师更稳妥的了。

莱昂哈德·欧拉是个听话的孩子。他甚至已经在巴塞尔大学注册了神学系。按照剧本，他会学习希腊语、希伯来语，研读经文，然后在某个宁静的教区度过一生，偶尔在布道词里引用几句哲学。

但巴塞尔当时住着一位并不安分的人物：约翰·伯努利。

约翰·伯努利当时是欧洲数学界的霸主之一，脾气暴躁，极度自负，并且对他那同样才华横溢的哥哥雅各布怀着一种复杂的竞争心理。对约翰来说，教书通常是件苦差事，尤其是教那些连微积分符号都认不全的大学生。

年轻的欧拉敲开了伯努利家的门。

我们不知道保罗·欧拉当时作何感想，但他应该注意到了儿子在神学课上的心不在焉。欧拉每个周六下午都会去伯努利家。这看起来像是去一个普通的补习班。

约翰·伯努利很快发现了一件怪事：这个年轻的神学生不需要他“教”。伯努利只给欧拉列书单，稍微点拨一下难点，下周六欧拉回来时，不仅弄懂了所有内容，甚至可能发现了一些伯努利自己都没注意到的细节。

伯努利是个骄傲的人，但他不瞎。他意识到如果让这个孩子去写布道词，将是人类文明的重大损失。于是，这位平时以刻薄著称的数学家做了一件温情的事：他亲自去拜访了保罗·欧拉。

没人知道那次谈话的具体细节。或许伯努利只是直白地告诉牧师：你的儿子属于数学，不属于讲坛。鉴于伯努利当时的名望，这就好比牛顿告诉一个家长“你儿子应该去搞物理”一样具有说服力。

保罗·欧拉妥协了。莱昂哈德·欧拉正式从神学转向数学。

圣彼得堡的赌局

1727年，欧拉二十岁。他在巴塞尔已经没有发展空间了。瑞士虽然安逸，但没有多余的教授职位。

就在这时，来自东方的邀请函到了。

俄国的圣彼得堡科学院刚刚成立。彼得大帝试图用金钱和头衔把西欧的科学家吸引到这片荒凉的沼泽地上，以此强行提升俄罗斯的科学水平。约翰·伯努利的两个儿子——丹尼尔·伯努利和尼古拉斯二世·伯努利——已经去了那里。

然而悲剧发生了。尼古拉斯二世·伯努利在圣彼得堡死于阑尾炎。丹尼尔极度孤独，写信给父亲，请求派欧拉过去做个伴，顺便填补科学院的空缺。

欧拉申请了。他得到的职位是：生理学部的医学士。

这听起来像个笑话。欧拉对医学的了解仅限于他在巴塞尔旁听的几节课。但他不在乎。只要能去有职位的地方，让他当厨师可能都行。为了在这份工作上显得称职，他在去俄国的路上突击阅读了大量解剖学和生理学书籍。

当他踏上圣彼得堡的土地时，情况比他预想的还要糟糕。

彼得大帝已经死了。他的继任者叶卡捷琳娜一世也在欧拉到达的那天奄奄一息。掌握实权的是一帮对科学毫无兴趣的官僚。他们看着这群花大钱请来的外国人，心里琢磨着怎么把他们赶走以节省开支。

科学院陷入了停滞。工资停发。研究经费冻结。

换做其他人，此时应该收拾行李回瑞士了。但欧拉没有。他在这种混乱中发现了一种奇怪的宁静。既然没人管他，也没人给他指派具体的医学任务，他索性躲进了数学部，回到了他最擅长的领域。

为了生存，他甚至接受了俄国海军的一个低级职位，负责教水手们怎么看星星导航。

右眼的代价

1735年，科学院给出了一个关于绘制俄国地图的任务。这是一个巨大的工程，涉及大量的天文观测和繁琐的计算。其他的院士们认为这需要几个月甚至几年才能完成。

欧拉说：三天。

没有人相信。这种计算量在没有计算机的时代，纯粹是体力的透支。

欧拉把自己关在房间里。三天三夜。他没有睡觉，手不停地在纸上移动。

三天后，他交出了结果。准确无误。

但他也倒下了。高烧，意识模糊，紧接着是一场严重的眼部感染。

当他从病床上爬起来时，医生告诉他一个坏消息：他的右眼几乎完全失明了。

对于一个学者，尤其是需要通过观测星空来校准数据的天文学家兼数学家来说，失去视力通常意味着职业生涯的终结。

欧拉的反应却平淡得让人害怕。他没有哭天抢地，没有抱怨命运不公。他只是调整了一下坐姿，稍微偏了偏头，用剩下的一只左眼看了看世界，然后说了一句后来被无数次引用的话：

“这样也好，以后分心的事就少了。”

这不是某种故作深沉的修辞。他是认真的。在他看来，外部世界的视觉信息往往是一种干扰。少了一只眼，意味着在这个三维世界里少了一半的视觉输入，大脑就能腾出更多的空间来处理抽象概念。

他在数学领域的产出不仅没有减少，反而开始加速。他开始涉足数论，去解决那个困扰了欧洲数学界几十年的“巴塞尔问题”。

巴塞尔问题很简单：所有自然数平方的倒数之和是多少？（即 1/1 + 1/4 + 1/9 + 1/16 + ...）

当时的数学家们能算出前几十项、几百项的和，大概是1.6449左右，但没人能给出一个精确的闭合形式。约翰·伯努利试过，莱布尼茨试过，都失败了。

欧拉用了那只剩下的左眼盯着这个问题。他没有像其他人那样试图去死算，而是把这个问题转化为了一个关于正弦函数的无穷多项式。

经过一系列在当时看来极其大胆、甚至在严谨性上有些“耍流氓”的操作，他得出了答案：

π²/6。

当这个结果公布时，数学界沉默了。把圆周率（π）引入到一个看似与几何毫无关系的级数求和问题中，这是什么道理。

这个答案确立了欧拉在欧洲数学界的地位。他不再是伯努利的学生，也不再是那个在俄国海军打杂的瑞士人。他是大师。

柏林的郁闷日子

1741年，俄国的局势再次恶化。普鲁士的新国王腓特烈大帝向欧拉伸出了橄榄枝。

腓特烈大帝自诩为“哲学家国王”。他在柏林建立科学院，希望能把那里变成欧洲的文化中心。他邀请了伏尔泰这样的思想家，当然也需要一位顶级的数学家来撑门面。

欧拉带着家人搬到了柏林。

一开始，一切看起来都很美好。薪水不错，但很快，欧拉发现自己遇到了一个新的问题：性格不合。

腓特烈大帝喜欢的是那种能在晚宴上谈笑风生、出口成章、充满机智和讽刺的文人。他喜欢伏尔泰那种尖锐的才智。

而欧拉？欧拉是个虔诚的加尔文教徒，生活作息规律，不爱出风头，说话直来直去。在柏林的沙龙里，当人们讨论自由意志、上帝是否存在、艺术的本质时，欧拉通常坐在一边，或者试图把话题引向刚体动力学。

太无聊了。腓特烈大帝开始在私下里嘲笑欧拉，叫他“数学维京人”或者“独眼巨人”。

在柏林的25年里，欧拉虽然在社交上被边缘化，但在学术上却处于巅峰。他出版了《无穷分析引论》。这本书基本上教全世界的数学家怎么正确地使用函数。

也就是在这里，他遇到了那个著名的“柯尼斯堡七桥问题”。

当时普鲁士有个叫柯尼斯堡的地方，河上有两个岛，七座桥把它们连接起来。当地居民闲着没事就在琢磨：能不能一次走遍这七座桥，每座桥只走一次，最后回到起点？

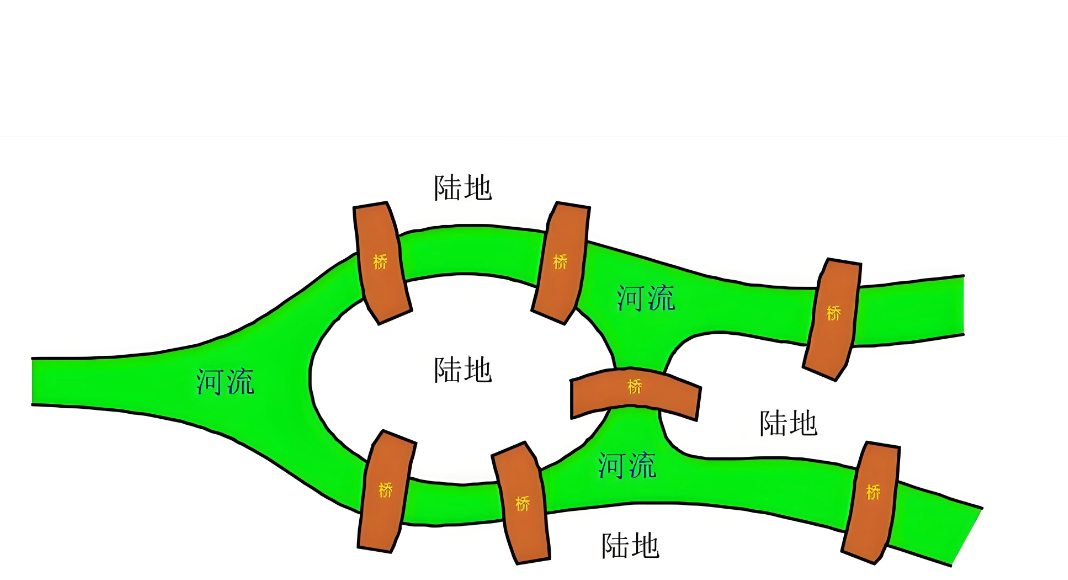
也没人能走出来，但也没人能证明走不出来。

这个问题被寄到了欧拉那里。

一开始，欧拉觉得这简直是在侮辱他的智商。“这种问题跟数学有什么关系？”他在信里抱怨道，“这是在考验一个人的腿脚，而不是大脑。”

但他还是忍不住去想。

他意识到，这个问题的关键不在于桥有多长，不在于岛的形状，也不在于河水流得有多快。关键在于连接的结构。

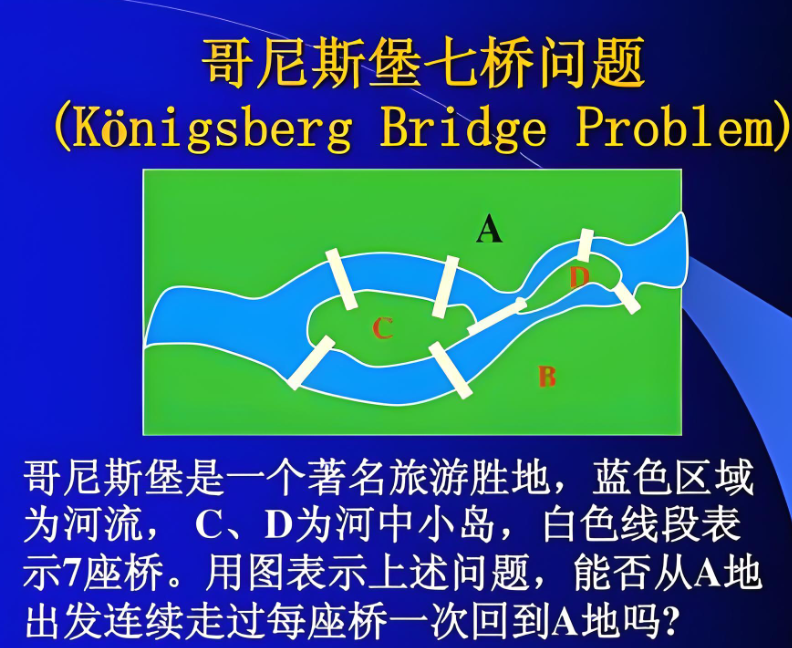
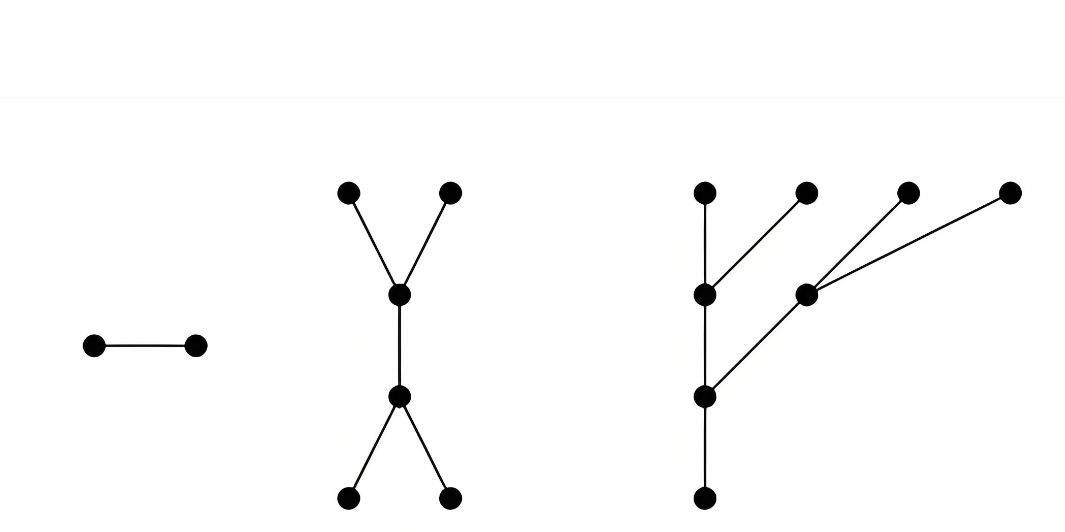
于是，他把陆地抽象成了“点”，把桥抽象成了“线”。

他没有去柯尼斯堡走一圈，他在纸上画了几个点和几条线，然后证明了：那些需要‘进出’的地方（比如小岛、路口），如果连接的路线是奇数条（比如 3 条、5 条），这种‘奇数连接点’最多只能有 2 个 —— 一个用来出发，一个用来结束。要是超过 2 个（比如柯尼斯堡有 4 个），就像出门后遇到好几条只能‘进不能出’或‘出不能进’的路，根本没法顺顺利利不重复走完全程，这事儿肯定办不成。”

欧拉大概只花了一下午时间就解决了这个问题，然后把它扔到一边，继续去算行星轨道了。

他并没有意识到，就在那个下午，他顺手创造了一个全新的数学分支：图论和拓扑学。这就是欧拉的风格：解决一个琐碎的谜题，然后不小心开创了一个学科。

尽管成果丰硕，柏林的气氛却越来越让人窒息。伏尔泰离开后，腓特烈大帝对欧拉的轻视变本加厉。他开始干涉科学院的事务，甚至试图教欧拉怎么管理数学部。

这就像是一个外行试图教乔丹怎么投篮。

1766年，60岁的欧拉受够了。尽管俄国依然充满不确定性，但那里有位新女皇——叶卡捷琳娜大帝——向他承诺了极高的待遇和绝对的尊重。

欧拉收拾行李，带着家人，回到了圣彼得堡。

黑暗降临

回到圣彼得堡没多久，灾难再次敲门。这一次，它要拿走剩下的那只眼睛。

欧拉仅存的左眼开始患白内障。视力急剧下降。在那个年代，白内障手术和酷刑没什么区别，而且成功率极低。

手术进行了。短暂的恢复后，感染随之而来。

几个星期内，黑暗彻底笼罩了他。

对于任何其他数学家，这都是终点。你需要看见公式，你需要检查推导过程，你需要查阅对数表。盲人怎么可能处理复杂的微积分？

但对于欧拉来说，这似乎只是稍微麻烦了一点。

欧拉拥有极其恐怖的记忆力。他能背诵整部《埃涅阿斯纪》，不仅能背，甚至能记得每一页的第一行和最后一行是什么。他知道前一百个素数的前六次幂是多少。

既然看不见纸，他就把计算过程全部在大脑中模拟。

他开始需要助手。通常是他的儿子，或者其他的年轻学生。工作流程是这样的：欧拉坐在椅子上，在脑子里推导公式，然后口述出来。助手在黑板上快速地记录。

这场景有点诡异。一个老头，坐在房间中央，嘴里念念有词：“假设x的平方加上...” 助手在旁边满头大汗地写。然后老头会突然停下：“等等，第三行那个符号写错了，应该是减号。”

他看不见，但他知道写错了。因为那个公式在他脑海里比在黑板上更清晰。

在这段完全失明的时期，他的产出率达到了生涯的最高峰。平均每周，他就能完成一篇高质量的论文。

1771年，圣彼得堡发生大火。大火蔓延到了欧拉的房子。

如果不是他的瑞士仆人彼得·格里姆冒死冲进火海，把这个盲眼老人背出来，欧拉可能就葬身火海了。

房子烧毁了。藏书烧毁了。家具烧毁了。

但抢救出了最重要的东西：他的手稿。

而在大火后的废墟上，欧拉甚至没有停顿太久。只要大脑还在，只要还能说话，数学就不会停止。他搬了新家，继续口述，继续计算。

这时期的欧拉已经不仅仅是一个学者，他成了一个神谕。欧洲各地的难题汇聚到圣彼得堡，然后答案从这个盲眼老人的房间里流出。

关于月球运动的理论？解决了；关于流体在管道中的阻力？算出来了；关于保险公司的年金计算？也搞定了。

他甚至抽出时间给孙女写了一本关于物理和哲学的科普书，这书后来成了欧洲的畅销书。

最后的一天

1783年9月18日。

这一天和往常没有什么不同。圣彼得堡的天气开始转凉。

上午，欧拉在思考关于气球上升的原理——那时候蒙特哥菲尔兄弟的热气球刚刚在巴黎引起轰动。即使在这个年纪，他对新事物依然充满好奇。

下午，他和家人吃了午饭。数学家安德斯·约翰·莱克塞尔来拜访他。

这两个人开始讨论刚刚发现的天王星的轨道问题。欧拉就在脑子里构建着这颗遥远行星的轨迹，和莱克塞尔交换着数据。

一切都很正常。他的思维依然敏锐，逻辑依然清晰。

下午五点左右，他喝了点茶。他还在抽着烟斗。

他在逗他的小孙女玩。

突然，那是极其突然的一瞬间，烟斗从他手中滑落。

他试图站起来，但身体失去了控制。他倒在地上。

在失去意识前的最后一刻，他非常平静地说了几个字：“我死了。”

这不是疑问句，不是惊叹句，是陈述句。就像他在陈述一个几何公理。

几个小时后，脑溢血带走了他。

法国哲学家孔多塞后来在悼词中写下了一句著名的结语，精准得如同欧拉自己的公式：

“...il cessa de calculer et de vivre.”（他停止了计算和生命。）

注意这个顺序。计算排在生命前面。

不朽的传奇

欧拉死后，圣彼得堡科学院陷入了恐慌。不是因为失去了领袖，而是因为他们不知道该怎么处理那堆遗稿。

弗斯秘书开始整理。一篇又一篇。一年又一年。

每当科学院的期刊觉得这期没什么好文章时，他们就会去那个“仓库”里拿一篇欧拉的存货。这招屡试不爽。

直到欧拉去世后的第80年，也就是1862年，瑞士自然科学协会决定要把欧拉的全集出版。他们以为这只是个大一点的项目。

这又是一个错误的估算。

《欧拉全集》（Opera Omnia）的编纂工作从1911年正式开始。原本计划出几十卷。

结果越编越多。直到21世纪初，这个项目才勉强接近尾声，总共出版了80多卷，每卷都是大开本，几百页厚，重得能砸死人。

你可以试一下：拿一本现在的数学或物理教科书，随机翻一页。你大概率会看到以“欧拉”命名的东西。

欧拉公式，被誉为上帝的公式。

欧拉示性数。

欧拉常数。

欧拉积分。

欧拉角。

欧拉线。

f(x)这个函数符号，他发明的。

Σ这个求和符号？他推广的。

e这个自然对数底？他定的。

i这个虚数单位？也是他标准化的。

如果把数学必做一座大厦，其他数学家可能负责砌了一面墙，或者修了一个漂亮的屋顶，或者挖了一个地基。

欧拉不是。欧拉是那个不仅提供了砖块、水泥，还顺便发明了起重机，并且编写了建筑规范的人。

他没有牛顿那种“天选之子”的压迫感，也没有高斯那种“生人勿进”的高冷。欧拉更像是一个极其勤奋、极其聪明、而且脾气还不错的工匠。他不在乎什么哲学意义，他只在乎这个公式好不好用，那个级数收敛不收敛。

在那个没有计算机、没有互联网、甚至连电灯都没有的时代，一个盲眼老头坐在圣彼得堡的寒风中，凭一己之力推演出了世界运行的底层逻辑。

这不科学。但这很欧拉。

免责提示：本文基于公开历史资料与技术文献整理，部分细节为叙事化演绎，仅供科普参考。